

Elizabeth P. · 1 · Nov 30 2014
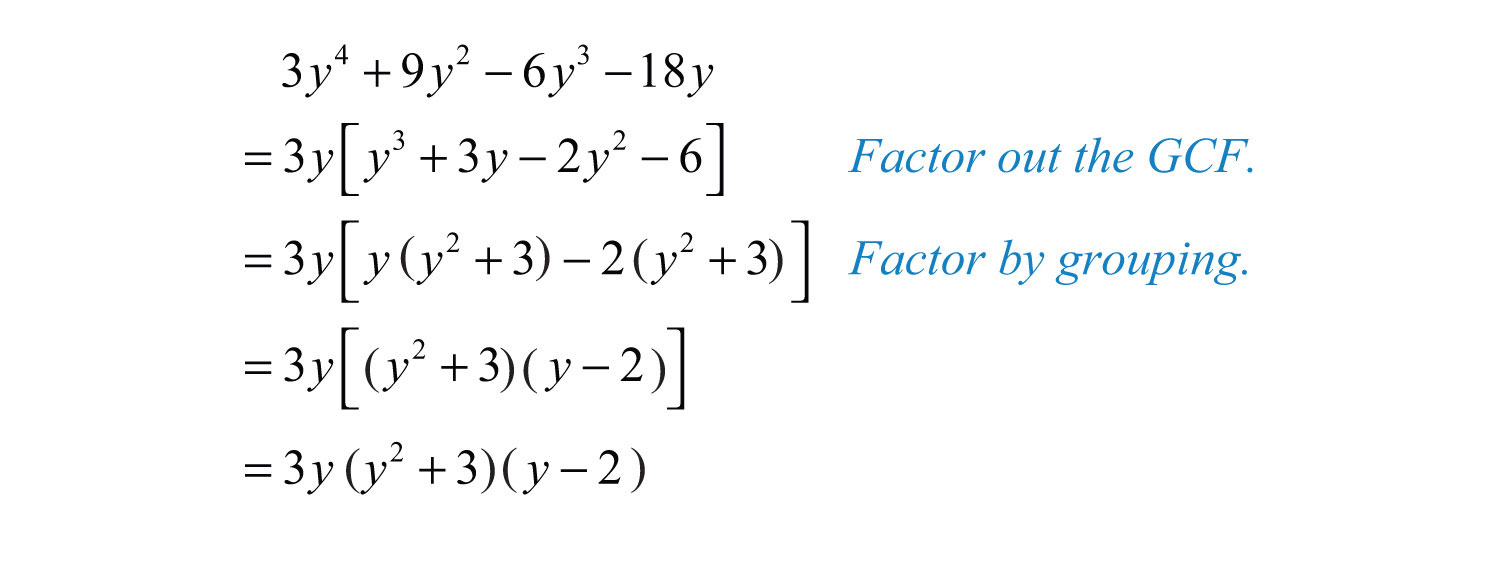
As you can see here we are making the terms inside the box brackets brackets into groups and then we remove the common factors. finally using the distributive property we write it as a product of 2 binomials.

Sidharth · 1 · Jan 11 2015
Please read below:
When we have a polynomial of the form #ax^2+bx+c# We can factor this quadratic with splitting up the #b# term into two terms. This allows us to factor the left side of the expression and the right side individually, and look for a common factor between them. This is factoring by grouping. Let's take our polynomial #ax^2+bx+c# again. To factor by grouping, we can rewrite this expression as #color(blue)(a)x^2+bx+color(red)(c)=color(blue)ax^2+(color(blue)a+color(red)c)x+color(red)c# Notice that #(a+c)x# is the same as our #b# term. We can distribute the #x# to both terms to get #color(blue)(ax^2+ax)+color(red)(cx+c)# This is the essence of factoring by grouping. We can look at our polynomial as two groups of two terms. From the blue terms, we can factor out an #ax# , and from the red terms, a #c# . This leaves us with #color(blue)(ax)color(purple)((x+1))+color(red)c color(purple)((x+1))# Now, both terms have an #x+1# in common, so we can factor that out to get #(color(blue)(ax)+color(red)(c))color(purple)((x+1))# We will not always have an #x+1# term. For instance, take the following polynomial: #3x^2+11x+6# Let's rewrite this as #color(turquoise)(3x^2+9x)+color(orange)(2x+6)# We can factor a #3x# out of the blue terms, and a #2# out of the orange terms. We get #color(turquoise)(3x)(x+3)+color(orange)2(x+3)# We can factor an #x+3# out to get #(3x+2)(x+3)# The key point is that we can rewrite our #b# term as the sum of two terms so we can factor twice. Next, we look for a common factor between our newly factored expression. Factoring by grouping will not always work- at this point it may be a good idea to resort to the Quadratic Formula. Hope this helps!

Jacobi J. · 1 · Jun 28 2018